The 2021 Grades 7 -8 Math Kangaroo Question Paper review

Given :

1) The number is in consecutive order from left to right
2) The number is in ascending order.

The method used to solve this problem is based on counting principles and combinatorics. Combinatorics is a branch of mathematics that deals with counting, arranging, and selecting objects,

To start, let us generate as many numbers as possible according to the given properties in this question. 1 observation we can make is that the final digit cannot be less than 4, as that would result in a number below 0. Similarly, the digit cannot exceed 9, as this would lead to a two-digit number. Consequently, the permissible options for the final digit are 4, 5, 6, 7, 8, and 9. This implies that we can create a total of 6 numbers.

To determine the percentage of the figure that is shaded in the case of concentric circles with lines passing through their common center, you would likely need to use geometric principles. Geometric principles involve the study and application of fundamental concepts and properties related to shapes, sizes, positions, and the spatial relationships between objects, providing a framework for understanding and solving problems in geometry.

Consider this question logically: if we divide the circle in half, you’ll notice that the white areas in one half perfectly correspond to the black spaces in the other. Therefore, if we were to overlay the black spaces from one half onto the white spaces in the other, we would observe that 50% or half of the circle is shaded.

Thus, making E our answer!

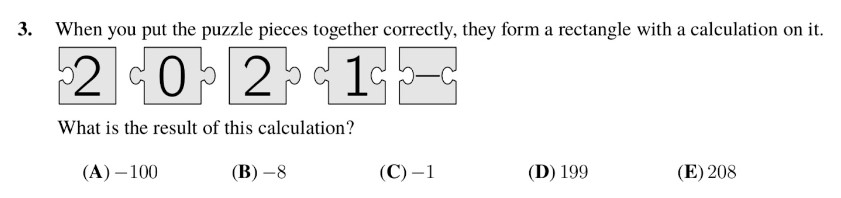
In analyzing this question, it becomes evident that the final puzzle pieces will be the edge pieces labeled 2 and 2. To establish a connection with the piece marked as 2, we require a puzzle piece with a left-sided inward projection, denoted by the symbol ‘-‘. Consequently, this particular puzzle piece should align with the 2 pieces.

Subsequently, we need a puzzle piece with an outward projection. Considering both options, 0 and 1, connecting the 0 proves incompatible with linking to the 1. Therefore, we must connect the 1 to the puzzle piece marked with ‘-‘. Following this logic, the piece labeled 2 should connect to 0.

In summary, the arrangement follows the sequence 2 – 102, resulting in the equation 2 – 102, which simplifies to -100.

Thus Making A the answer!!

This problem involves knowing about Volume, Dimensions and symmetry. Volume is the amount of space occupied by an object, and it is measured in cubic unit

s. Dimensions refer to the measurements that define the size and shape of an object, usually represented by its length, width, and height in three-dimensional space.Symmetry is a property in which an object or a shape looks the same when certain transformations, such as reflection, rotation, or translation, are applied to it. In simpler terms, if you could fold, turn, or slide an object, and it still appears unchanged, it is considered symmetrical.

Shapes B, C, and E exhibit symmetry, meaning they have a central axis along which the forms are mirror images of each other. In such cases, when water is poured into these vases, the level will rise evenly up to the line of symmetry. However, Shapes A and D lack this symmetry.

For Shape A, as there is no line of symmetry, the water distribution will be uneven. The midpoint of the vase will have a higher water level because the bottom portion does not hold as much water as the upper part.

On the other hand, Shape D’s lack of symmetry implies that the water level will not rise uniformly. The midpoint will be lower since the wider bottom of the vase has a greater capacity to hold water compared to the narrower top.

In conclusion, due to the absence of symmetry, Shapes A and D will exhibit non-uniform water levels. Among them, Shape A is expected to have the highest water level, as its midpoint will likely be elevated due to the reduced capacity at the bottom.

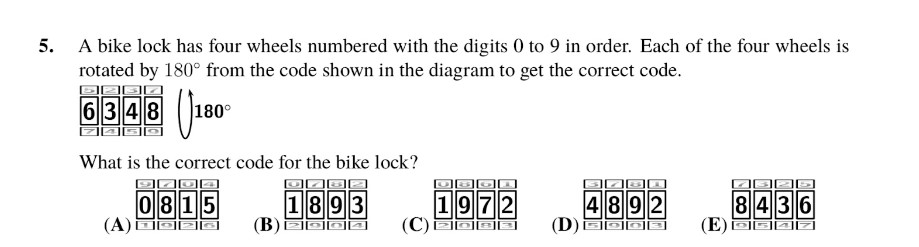
Let us employ a guess-and-check method for this problem.

Starting with option A, the transition from 6 to 0 requires 6 turns, while the shift from 3 to 8 demands 5 turns, making option A unsuitable.

Moving on to option B, the change from 6 to 1 involves 5 turns, and similarly, the transition from 3 to 8 also requires 5 turns. This consistency suggests that option B is a viable answer, but it’s prudent to assess the other choices for confirmation.

Considering option C, the journey from 6 to 1 takes 5 turns, yet moving from 6 to 9 demands 7 turns, making option C improbable.

Now, evaluating option D, the shift from 6 to 4 necessitates 2 turns, but transitioning from 6 to 8 demands 8 turns, rendering option D implausible.

Lastly, examining option E, the transition from 6 to 8 requires 8 turns, whereas moving from 3 to 8 involves 5 turns, indicating that option E is not the answer.

Consequently, through this process of elimination, it is determined that option B is the most fitting solution for this question.

The approach to solving this problem involves a combination of algebraic manipulation and logical deduction. It utilizes the given relationships between the letters (A, B, C, D) to determine the values they represent, specifically the sums of B and D and A and C.

In addressing this question, we observe that the sum of B and D is 7, while the sum of A and C is 13. Keeping this information in mind, we proceed to solve ADCB + CBAD. Since B and D together equal 7, the last digit is determined to be 7. Now, focusing on A and D, which sum to 13, and considering the carryover to the tens place, it should be 3. Eliminating choices with a last digit of 4, we are left with D and B. Considering the carryover of 1, the hundred place becomes 8. Therefore, B emerges as the answer.

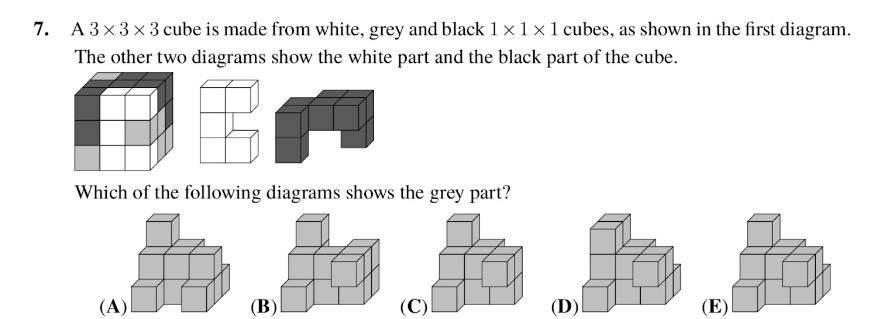
To solve this problem we can analyze the characteristics of the cubes presented and deduce a logical pattern.

We can observe that the gray section displays a zigzag pattern, with only cubes D and E exhibiting this pattern. Furthermore, atop the pattern, there is a single cube, indicating that E is likely the correct answer.

If Neil consumed 12 squares from two rows, it implies that from one row, there are 6 squares. Additionally, it’s mentioned that another size comprises 9 squares. Combining the 9 squares with the remaining two strips results in a deduction of 12 squares. Thus, subtracting 21 from 66 yields 45, indicating that D is the correct answer.

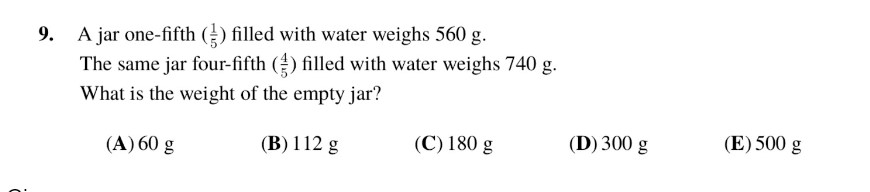
Given:

A jar one-fifth filled with water weighs 560 g.
The same jar four-fifth filled with water weighs 740 g.

We denote the weight of the empty jug as X and the weight of the water that can be filled in the jug as Y.

First, we set up our equations:
– From the first scenario where one-fifth of the jug is filled, we have the equation (X+Y) /5 = 560
– From the second scenario where four-fifths of the jug is filled, we have the equation (X+ 4Y) /5 = 740

To eliminate the fraction, we multiply the first equation by 4, yielding (4X + 4Y)/5 = 2240 .

Now, we subtract the second equation from the modified equation 1 to solve for X, In which we get 3X=1500.

Solving for X, we get X = 500.

Thus, the weight of the empty jug is 500 grams, making option E the correct answer.

We can infer that the triangle occupies ¼ of the square’s area. Consequently, the square’s area is 16, and the triangle’s area is 4. If we sum up the areas of the square and the triangle, considering there are two of each, the total becomes 48. Therefore, B is the correct answer.

To solve this problem we can use our basic arithmetic operations, namely addition, subtraction, multiplication, and division

Given:
– There are 25 planks of wood.
– Each plank measures 30 cm in length.
– The total length of all the planks is \(25 \times 30 = 750\) cm.

We’re also given that 6.9 meters is equal to 690 cm.

To find the length of the overlap between any pair of adjacent planks, we first calculate the total length of the overlap. We can do this by subtracting the length of 6.9 meters (690 cm) from the total length of the planks (750 cm):

750 cm – 690 cm=60cm

Now, we need to distribute this 60 cm of overlap among the 24 seams between adjacent planks. Since there are 25 planks but only 24 seams between them, we divide the total overlap length by 24:

60/24 = 2.5

Therefore, the length in cm of the overlap between any pair of adjacent planks is indeed 2.5 cm. So, the answer is B.

To solve this problem we can use basic principles of geometry and arithmetic operations

Given that there are 5 identical right-angled triangles, we can calculate the measure of the larger acute angle by dividing the total angle measure of 360 degrees by the number of triangles, which gives us 72 degrees.

Subtracting 72 degrees from the right angle (90 degrees), we find that the smaller acute angle measures 18 degrees.

Now, to find out how many times the smaller acute angle fits into a full circle (360 degrees), we divide 360 by 18, which equals 20.

Therefore, option D is the correct answer.

We can see that the length of the smallest square is 1. Looking at the 2nd smallest square we see that the side is increasing by 0.5 thus making the 2nd square side be 1.5. Next let’s look at the 3rd largest square, we can see that the side length is 2.5 (1+1.5). Next, looking at the 2nd largest square we can see that the side length is 3.5(2.5 +1) . Lastly looking at the largest square we can see that the side length is 4.5 (3.5 +1) But reducing the 0.5 we can see that H is equal to 4 thus making C the answer.

To solve this problem we can use our knowledge about the systems of equations. A system of equations is a collection of two or more equations involving the same set of variables, typically used to find the values of those variables that satisfy all the equations simultaneously.

x = number of questions that are correct
y = number of wrong answers
z = number of questions left blank
x,y,z are nonnegative whole numbers.

Since there are 20 questions total, this means the first equation to set up is:
x+y+z = 20

Solving for y leads to
x+y+z = 20
y+z = 20-x
y = 20-x-z

We’ll use this later.

Another equation to set up is 7x-4y = 100 because Eric earns 7 points per correct answer and loses 4 points for each incorrect answer, and all that leads to 100 points total which was his quiz score. We’ll ignore the questions he left blank since they add 0 points.

Let’s plug the equation in which we isolated y

7x-4y = 100
7x-4(20-x-z) = 100
7x-80+4x+4z = 100
7x+4x+4z = 100+80
11x+4z = 180

Now we can use the guess and check method to see which pair of x and z values will make that last equation above true. I suggest starting with the smallest possible value of x and using that x value to solve for z.

If x = 0, then,
11x+4z = 180
11(0)+4z = 180
4z = 180
z = 180/4
z = 45

So if Eric got 0 correct answers, then he left 45 questions blank. But that isn’t possible because there are only 20 questions total. So we’ll ignore the case that x = 0.
If we increase x by 4, and decrease z by 11, then we get another ordered pair solution to this equation
So another solution is (x,z) = (4,34)

Note that
11x+4y = 180
11(4) + 4(34) = 180

But like before, z = 34 isn’t possible since 20 is the max.

Increase x by 4 again, and drop z by 11 to get (x,z) = (8,23). Again we run into the same issue as before.

Increase x by 4 again, and decrease z by 11 to get (x,z) = (12, 12). Now we have both x and z smaller than 20, but note how x+z = 12+12 = 24 which exceeds the total number of questions. So we rule this case out as well.

Do another round of “increase x by 4, decrease z by 11” to get to (x,z) = (16, 1). This is the only case left because anything beyond this, z will be negative.

Luckily, this final case does work. If Eric answers x = 16 questions correctly, then he left z = 1 of them blank. That must mean y = 20-x-z = 20-16-1 = 3 questions were incorrect.
We can see that:

7x-4y = 7(16)-4(3) = 112-12= 100
meaning that (x,y) = (16,3) is a solution to 7x-4y = 100.

To summarize, we found that the only possible solution is (x,y,z) = (16, 3, 1)
Meaning x = 16 questions were correct, y = 3 were wrong, and z = 1 question was left blank.

Thus making B the answer

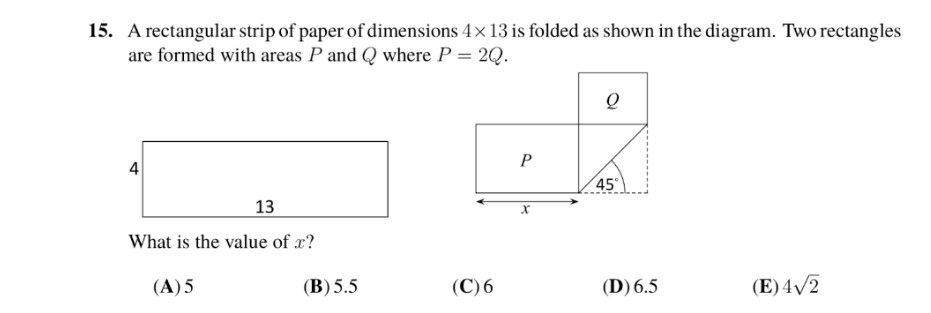
So we see that the rectangle has an area of 52 and we see that when they are bending it the 13 is getting cut by 2 which is giving you the X thus 13/2 = 6.5

Making D the answer.

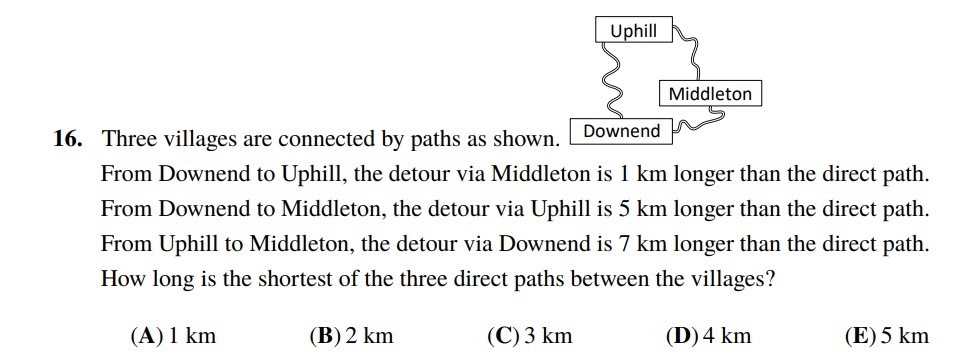
Given:
– From Downend ( D ) to Uphill ( U ), the detour via Middleton ( M ) is 1 km longer than the direct path.
– From Downend ( D ) to Middleton ( M ), the detour via Uphill ( U ) is 5 km longer than the direct path.
– From Uphill ( U ) to Middleton( M ), the detour via Downend ( D ) is 7 km longer than the direct path.

Lets us change the equations above to something like this :

( D plus M ) + ( M plus U ) = ( D plus U ) + 1
( D plus U ) + ( U plus M ) = ( D plus M) + 5
( U plus D ) + ( D plus M ) = ( U plus M ) + 7

Now, We need to find the shortest of the three direct paths between the villages.

Let’s denote:
– ( x ) as the length of the direct path from Downend to Uphill/ Uphill to Downend
– ( y ) as the length of the direct path from Middleton to Uphill/Uphill to Middleton.
– ( z ) as the length of the direct path from Downend to Middleton/ Middleton to Downend

Given the detour information:
1. ( x + 1 = y + z )
2. ( y + 5 = x + z)
3. ( z + 7 = x + y)

Now, let’s add all of these together!!

x + y + z + 13 = x + y + z + x + y + z
x + y + z + 13 = x + y + z + x + y + z
x + y + z = 13
y + z = 13 – x

Now, let’s substitute the y + z by looking at Equation number 1:
[ x + 1 = y + z ] [ x + 1 = 13 – x ] [2x = 12] [x = 6]

So, we know that x = 6

Now, looking back at the sum of our detour information: x + y + z = 13
[x + y + z = 13] [x + z = 13 – y]

Now, let’s substitute the x + z by looking at Equation number 2:
[y + 5 = x + z] [y + 5 = 13 – y] [2y = 8] [y = 4]

Now, looking back at the sum of our detour information: x + y + z = 13
[ x + y + z = 13] [6 + 4 + z = 13] [Z = 3]

Thus making Z the answer

To solve this problem we can use our knowledge of Algebraic manipulation involving rearranging equations and using properties of algebra to solve for unknown variables or expressions.

We know that the original fraction is a/b, and the numerator is increased by 40% to become 1.4a

To make the new fraction double the original fraction, we have:

2 * a/b =1.4a/b-x

where ( x ) represents the percentage decrease in the denominator.

Expanding this equation:

2a/b =1.4a/b-x

Cross-multiplying:

2a(b – x) = 1.4ab
2ab – 2ax = 1.4ab

0.6ab = 2ax
x = 0.6ab/2a(we can cancel out the a’s)
x = 0.6b/

\[ x = 0.3b \]

So, x = 0.3b , which means a decrease of 0.3 times the original denominator b.

Now, to convert 0.3 into a percentage we have to multiply it by 100 giving us 30%

Therefore, the correct answer is that the denominator should be decreased by 30% so that the new fraction is double the original fraction.

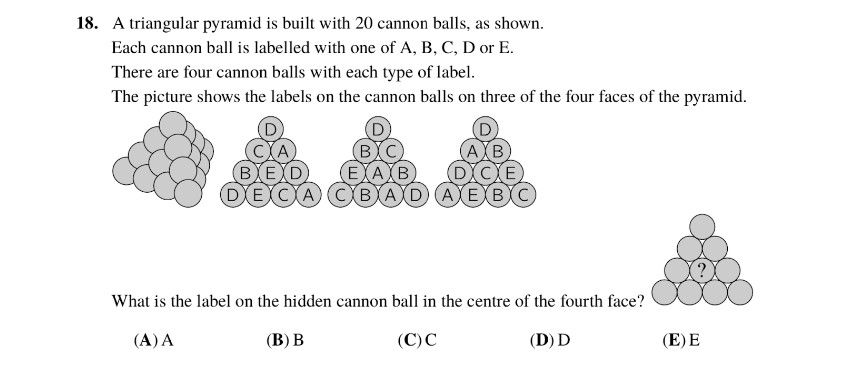
Given that there are 4 balls with the same alphabet on them, and we observe the count of each letter:

– 4 A’s
– 4 B’s
– 4 C’s
– 3 D’s
– 4 E’s

We need to determine which letter has a count different from the others. Based on the counts given, it’s evident that the letter “D” has a count of 3, whereas all other letters have a count of 4.

Therefore, “D” is indeed the answer, as it deviates from the pattern established by the other letters, making it the odd one out.

2ABCDE ×3 = ABCDE2

Starting from right we get,
E * 3 = 2 in last
E = 4
so, 4 * 3 = 12 (1 carry)

now,
2ABCD4 ×3 = ABCD42
we get,
D * 3 + 1 = 4 in last
D * 3 = 4 – 1 = 3
D = 1 .

putting this value also,
2ABC14 ×3 = ABC142
we get,
3 * C = 1 in last
C = 7
3 * 7 = 21 then 2 is carry .
putting this value also,
2AB714 ×3 = AB7142

we get,
3 * B + 2 = 7
3 * B = 5
B = 5

1 carry { 3 * 5 = 15 }
putting this value also,

2A5714 ×3 = A57142
we get,
A * 3 + 1 = 5
A * 3 = 5 – 1 = 4
A = 8

finally we get,
285714 ×3 = 857142

therefore,
→ 2 + A + B + C + D + E
→ 2 + 8 + 5 + 7 + 1 + 4
→ 27 (B) (Ans.)

Given that there are 2021 kangaroos numbered from 1 to 2021, and each kangaroo is colored either red, grey, or blue such that every three consecutive kangaroos contain all three colors, we need to determine which of Bruce’s guesses about the colors of five specific kangaroos is incorrect. Bruce’s guesses are:
– Kangaroo 2 is grey.
– Kangaroo 20 is blue.
– Kangaroo 202 is red.
– Kangaroo 1002 is blue.
– Kangaroo 2021 is grey.

We know that exactly one of these guesses is wrong. To solve this, let’s establish a pattern for the colors of the kangaroos based on the given constraint that every set of three consecutive kangaroos contains all three colors.

Step-by-Step Analysis:

1. **Identify the Color Pattern**:
Since every set of three consecutive kangaroos must include all three colors, a feasible pattern for the colors can be cyclical. Let’s use the sequence Red (R), Grey (G), Blue (B) as an example. If this cycle repeats, it will cover every three consecutive kangaroos without repetition:
– Kangaroo 1: R
– Kangaroo 2: G
– Kangaroo 3: B
– Kangaroo 4: R
– Kangaroo 5: G
– Kangaroo 6: B
– …

2. **Verify Bruce’s Guesses with the Pattern**:
– Kangaroo 2 (G): According to the pattern, Kangaroo 2 should indeed be Grey (G).
– Kangaroo 20 (B): Since the cycle repeats every three kangaroos, we calculate the color of Kangaroo 20. The position 20 modulo 3 gives us 2, implying that Kangaroo 20 should be Grey (G), not Blue (B).
– Kangaroo 202 (R): Calculating modulo 3, 202 modulo 3 is 1, so Kangaroo 202 should be Red (R).
– Kangaroo 1002 (B): Similarly, 1002 modulo 3 gives us 0, so Kangaroo 1002 should be Blue (B).
– Kangaroo 2021 (G): Calculating modulo 3, 2021 modulo 3 is 1, indicating Kangaroo 2021 should be Red (R).

Conclusion:
– Based on our pattern:
– Kangaroo 2 is indeed Grey (correct guess).
– Kangaroo 20 is not Blue; it should be Grey (incorrect guess).
– Kangaroo 202 is correctly guessed as Red.
– Kangaroo 1002 is correctly guessed as Blue.
– Kangaroo 2021 is not Gray; it should be Red (incorrect guess).

Determine the Incorrect Guess:
Since Bruce made only one incorrect guess, and Kangaroo 20 was guessed to be Blue (which should be Grey), and Kangaroo 2021 should be Red but was guessed as Grey, we see that Bruce can only make one mistake. The pattern correctly identifies one mistake:
– Kangaroo 20 being Blue is the mistake because it should be Grey.

Thus, the number of the kangaroo whose color Bruce guessed incorrectly is:

20

Let:
– (C) be the price of cherries in shop C.

Step-by-Step Analysis

1. **Price in Shop B**:
The price in shop B is 20% lower than in shop C:
B = C – 0.20C = 0.80C

2. **Price in Shop A**:
The price in shop A is 25% higher than in shop B:
A = B + 0.25B = 1.25B

Substituting B from the previous step:
A = 1.25 \times 0.80C = 1.00C

3. **Price in Shop D**:
The price in shop D is 30% higher than in shop C:
D = C + 0.30C = 1.30C

Comparing Prices Between Shops D and A

Now, let’s compare D and A
– From the above, we have A = 1.00C and D = 1.30C .

To find the relation between D and A:
D = 1.30X = 1.30A

This means that the price in shop D is 30% higher than the price in shop A.

Amelia’s transformation rule is that each number is replaced by the difference between the number and the sum of its digits. Let’s analyze how this transformation affects the numbers from 1 to 100.

Step-by-Step Analysis:

1. **One-digit Numbers (1 to 9)**:
– For any one-digit number n the sum of its digits is equal to the number itself.
– So, when we subtract the sum of digits from the number, we get n-n=0.
– Thus, for one-digit numbers, the result of the transformation is always 0.

2. **Two-digit Numbers (10 to 99)**:
– For a two-digit number ( n ), let’s denote its digits as a and b
– The sum of its digits is a+b
– So, the result of the transformation is ( n – (a + b) ), which simplifies to 9a where a ranges from 1 to 9 (since n is a two-digit number).
– This gives us the transformed numbers: 9, 18, 27, 36, 45, 54, 63, 72, and 81.

3. **Number 100**:
– The sum of its digits is 1 (1 + 0 + 0).
– So, the result of the transformation is \( 100 – 1 = 99 \).

Conclusion:

Collecting all the unique transformed numbers:
– From 1 to 9: ( 0 ).
– From 10 to 99: ( 9, 18, 27, 36, 45, 54, 63, 72, 81 ).
– From 100: ( 99 ).

So, there are ( 1 + 9 + 1 = 11 ) different numbers obtained.

We observe that each pentagon is connected to 5 hexagons, giving us a ratio of 1 pentagon to 5 hexagons. Since there are 12 pentagons, multiplying 12 by 5 gives us 60 hexagons. However, this isn’t our final answer. Each hexagon is connected to 3 pentagons, so we need to divide 60 by 3, which equals 20. Therefore, our final answer is 20 hexagons.

This problem involves deductive reasoning and arithmetic to find the solution. Given the number of knights and knaves in a town, along with the arrangement of pairs described by each other, we deduce the composition of the pairs. Since each pair consists of one knight and one knave, and we know the total number of knights and knaves, we infer that the unpaired individuals must all be knights. By dividing the total number of unpaired knights by 2, we find the number of pairs of two knights, which gives us the answer to the problem.
‘
Let’s break down the problem:

1. There are 21 knights who always tell the truth and 2000 knaves who always lie.
2. A wizard divided 2020 of these 2021 people into 1010 pairs.
3. Each person in a pair described the other person as either a knight or a knave.
4. 2000 people were called knights, and 20 people were called knaves.

Since each pair consists of one knight and one knave, and there are 2020 people in pairs, this accounts for 2020 knights and 2020 knaves.

Now, since 2000 people were called knights and 20 were called knaves, we can deduce that the 2020 pairs involved 2000 knights and 20 knaves.

This leaves 1980 knights unpaired.

Given that knights always tell the truth and knaves always lie, the 1980 unpaired individuals must all be knights.

Therefore, out of the remaining 1980 knights, we need to find how many pairs of two knights we can form.

{Number of pairs of two knights} = 1980/2 = 990]

So, there were 990 pairs of two knights.

The answer is (C) 990.

Given:
1. Triangle (ADC) is equilateral.
2. The area of triangle (ADC) is half the area of triangle \(ABC\).

Key Points

1. **Equilateral Triangle (ADC)**:
– Since (ADC) is equilateral, all its sides are equal.
– Let (AD = DC = s).

2. **Area Relationship**:
– The area of (ADC) is half of (ABC).

Visualizing the Triangles

1. Point (D) lies on side (AB) such that (AD = DC = s).
2. Let (DB = x).

3. Since triangle (ADC) is equilateral and its area is half the area of \(ABC\), \(D\) divides \(AB\) in such a way that the base of triangle \(ABC\) doubles the base of triangle \(ADC\).

Geometric Relationship

1. In triangle (ADC), all internal angles are 60 degrees because it’s equilateral.
2. Since triangle ABC has the area exactly twice that of ADC and point D divides AB into two equal parts, triangle ABC must also maintain symmetry around D

Angle Calculation

1. angle CAD = angle ADB = 60 Degrees) since triangle ADC is equilateral.
2. The remaining angle at (B) within the triangle ABC is split by D equally.

Given the area relationship, angle CBA must be half of the 120degrees (from symmetry in triangle properties), so:
CBA=30degrees

Therefore, the measure of angle CBA is30degrees
Thus making D the answer

https://parinama.academy/wp-content/uploads/2024/08/Question-26-.jpg

Problem Statement

You have a box containing green, red, blue, and yellow tokens. There are several constraints on the number of each color of tokens when choosing a subset of them:

At least one green token among any 27 chosen tokens.
At least one red token among any 25 chosen tokens.
At least one blue token among any 22 chosen tokens.
At least one yellow token among any 17 chosen tokens.

Objective

Find the maximum number of tokens (total) in the box.

Variables
Let’s define:
ggg: Number of green tokens.
rrr: Number of red tokens.
bbb: Number of blue tokens.
yyy: Number of yellow tokens.

Constraints Translated into Inequalities

If at least one green token is always present among any 27 tokens chosen, then the number of non-green tokens must be less than 27: r+b+y≤26

If at least one red token is always present among any 25 tokens chosen, then the number of non-red tokens must be less than 25: g+b+y≤24

If at least one blue token is always present among any 22 tokens chosen, then the number of non-blue tokens must be less than 22: g+r+y≤21

If at least one yellow token is always present among any 17 tokens chosen, then the number of non-yellow tokens must be less than 17: g+r+b≤16

Combining Inequalities

We have these four inequalities:
r+b+y≤26
g+b+y≤24
g+r+y≤21
g+r+b≤16

To find a common upper limit, we add these inequalities together:
(r+b+y)+(g+b+y)+(g+r+y)+(g+r+b)≤26+24+21+16

Simplifying the Left Side

When we add the left sides of the inequalities, we get:
r+b+y+g+b+y+g+r+y+g+r+b

Combine like terms:
3g+3r+3b+3y3g + 3r + 3b + 3y3g+3r+3b+3y

Simplifying the Right Side
Adding the right sides of the inequalities:

26+24+21+16 = 8726 + 24 + 21 + 16 = 8726+24+21+16=87

So the inequality now is:
3g+3r+3b+3y ≤ 87

Dividing by 3
To simplify:
g+r+b+y ≤ 29

Conclusion :
The largest number of tokens that can be in the box, satisfying all the given constraints, is 29.
Thus, the maximum number of tokens in the box 29

Let’s solve this problem by organizing the matches while ensuring each team plays only once per round. Our objective is to find out in which round D plays against F.

Given Matches

Round 1: A−BA – BA−B
Round 2: C−DC – DC−D
Round 3: A−EA – EA−E
Round 4: E−FE – FE−F
Round 5: A−CA – CA−C

Teams and Possible Matches
Teams: A, B, C, D, E, F
Total possible matches: {(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)}

Filling the Schedule

We need to ensure each round has exactly 3 matches, and no team plays more than once per round.

Round 1: A−BA – BA−B
Remaining teams: C, D, E, F
Possible matches: C−E and D−F

Round 1 matches: A−B,C−E,D−F

Round 2: C−D
Remaining teams: A, B, E, F
Possible matches: A−F and B-E

Round 2 matches: C−D,A−F,B−E

Round 3: A−E
Remaining teams: B, C, D, F
Possible matches:B−D and C−F

Round 3 matches: A−E,B−D,C−F

Round 4 – E – F
Remaining teams: A, B, C, D
Possible matches: A−D and B-C

Round 4 matches: E−F,A−D,B−C

Round 5: A−C
Remaining teams: B, D, E, F
Possible matches: B−F and D-E
Round 5 matches: A−C,B−F,D−E

Verify When D Plays F

From the above rounds:
Round 1: D−F
Round 2: C−D
Round 3: B−D
Round 4: A−D
Round 5: D−E
Team D plays against team F in Round 1.
Thus, the answer is 1

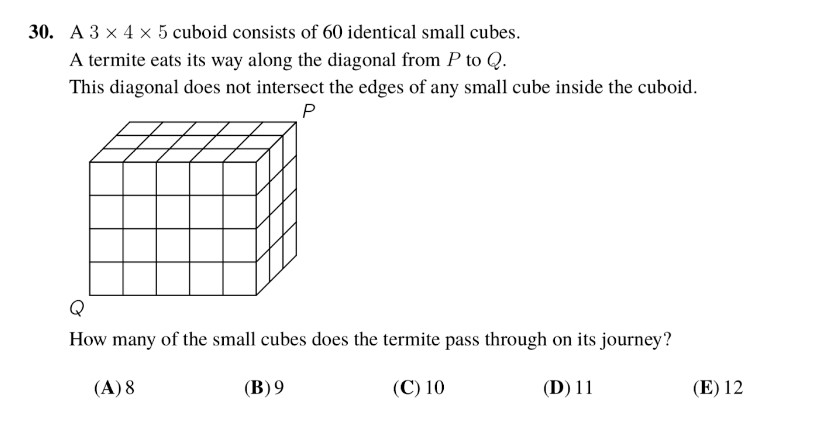
Step-by-Step Method

Cuboid Dimensions:
Height (aaa) = 3
Width (bbb) = 4
Length (ccc) = 5

Understanding the Path:
The termite starts at one corner and moves to the opposite corner diagonally.
The termite will cross from one small cube to another each time it crosses a plane defined by the cuboid’s dimensions.

Counting Crossings:
We need to count the number of times the termite crosses the internal planes of the cuboid.
Think of the Path in 2D:
Imagine how the termite moves in the x, y, and z directions separately. It will cross boundaries in each direction.

Counting Crosses in Each Dimension:
Height (3 layers): The termite will move from the bottom layer to the top, crossing 2 internal horizontal planes (3 layers – 1).

Width (4 columns): The termite will move from one side to the other, crossing 3 internal vertical planes (4 columns – 1).

Length (5 rows): The termite will move from one end to the other, crossing 4 internal vertical planes (5 rows – 1).

Combine the Crosses:
Total crosses: 2 (height) + 3 (width) + 4 (length).

Adding the Crosses
Simply add the number of times the termite crosses planes in each dimension: 2+3+4=92 + 3 + 4 = 92+3+4=9

However, we need to account for where these planes intersect each other. Each crossing at an intersection of planes counts as one less because we are not crossing into a new cube each time we hit an intersection of these planes.

Imagine moving from one corner to the other in three straight steps:
From one corner to the far corner, we change all three coordinates (x, y, and z).

Think of it like this:
First step changes one coordinate (e.g., x).
Second step changes another coordinate (e.g., y).
Third step changes the last coordinate (e.g., z).

Crosses in Dimensions:
Start at (0,0,0) and move to (3,4,5).
Each time you step in the x, y, or z direction, you enter a new cube.
But, remember you overlap crossings where:
x and y intersect (width and height).
x and z intersect (width and length).
y and z intersect (height and length).
For simplicity, this approach adds back:
333 + 444 + 555 moves minus the overlaps:

Simplified Counting:

Diagonal Path: Cross all three dimensions: 3+4+5−2=10
Conclusion

Thus, the termite passes through 10 cubes on its journey from PPP to QQQ.