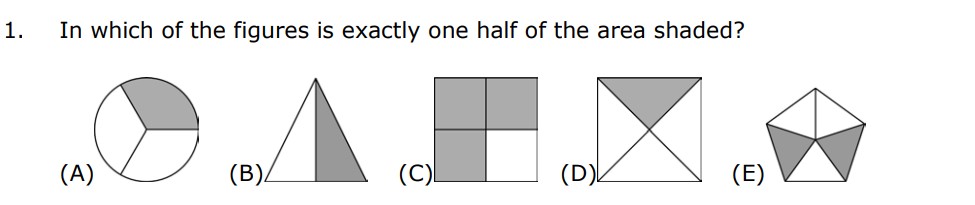
After reading the question you can see that they are asking for the figure that has exactly one half of their area shaded.
If we look at A) we can see that in the circle ⅓ of its area is shaded so A can not be the answer
If we look at B we can see that in the triangle ½ of its area is shaded so that means B should be the answer but even though we know what the answer is let’s clarify by checking C, D and E to
If we look at C we can see that in the square ¾ of its area is shaded so C can not be the answer
If we look at D we can see that ¼ of the square area is shaded so D can not be the answer
If we look at E we can see that ⅖ of the pentagon area is shaded so that means E can not be the answer
So that means for this question B Is the answer
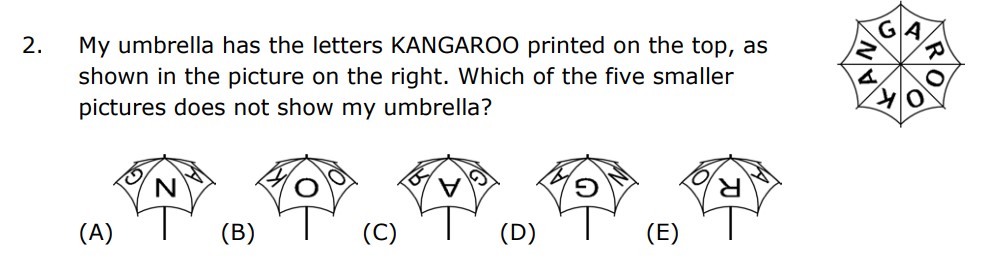
After reading the question you can see that they are asking the picture that DOES NOT show their umbrella (the picture is on the right of the question)
If we look at A we can see that the umbrella is showing the letters A N G and if we look at the umbrella picture on the right we can see that A is a possible solution making A not be the answer
If we look at B we can see that the umbrella is showing the letters O O K and if we look at the umbrella picture on the right we can see that B is a possible solution making B not be the answer
If we look at C we can see that the umbrella is showing the letters G A R but the R is the mirror image of a normal R and you can search the umbrella but you can not find it making C be the answer.
If we look at D we can see that the umbrella is showing the letters N G A and if we look at the umbrella picture on the right we can see that D is a possible solution making D not be the answer
If we look at E we can see that the umbrella is showing the letters A R O and if we look at the umbrella picture on the right we can see that E is a possible solution making E not be the answer
So that means C is the answer

So let’s start by creating an equation. (1 duck * 1 egg * 1 day) * 10 so for a course of 10 days 1 duck will lay 10 eggs and if we multiply by 5 since there are 5 ducks we will get 50
Now the next part of the equation says that 5 ducks out of the 10 ducks each Lay an egg every 2 days for a period of 10 days. Let’s also create an equation for this to make it easier. We see that the ducks will lay eggs on 5 days since 10/2 = 5 we are doing this because the ducks are laying eggs every 2 days. So (1 duck * 1 egg * 1 day) *5 and we will multiply by 5 since there are 5 ducks we will get 25
so if we add 50 and 25 we have our answer which is 75 making A the answer.
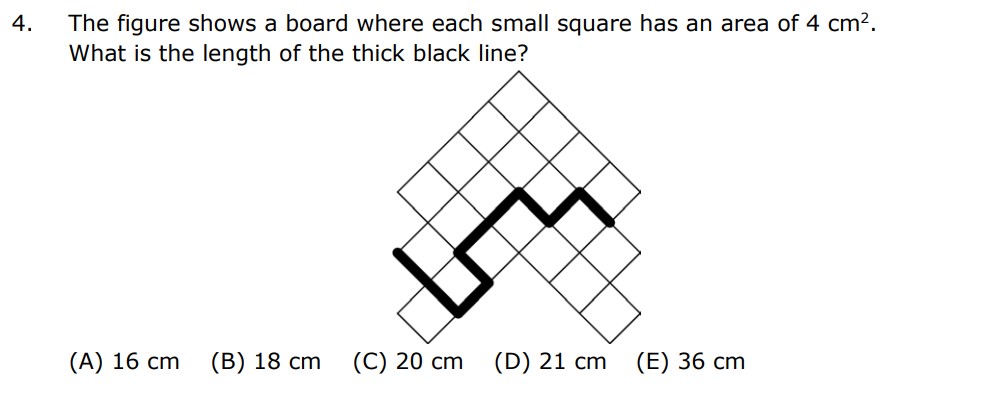
So we know that to find an area of an square the formula is a squared and we know that the area is 4 so we can create the equation
a^2= 4, now we can make this equation , a squared = 2 squared and since both of them go to the power of 2 we can cross them out making a = 2 and right one a is representing the side of the square and since there are 9 shaded sides of the square ( 9*2) 18 is the answer making B be the answer.
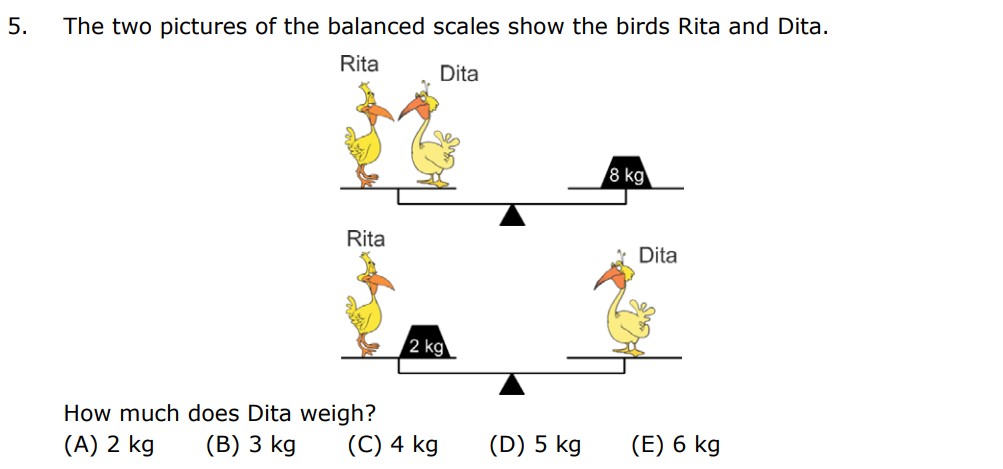
Given:
Rita + Dita = 8 kg
Rita + 2kg = Dita
Let’s create an equation for each of these scales
In the first scale, Rita and Dita are equal to 8kg, that makes the equation,
Equation 1 = > R + D = 8
In the second scale, Rita + 2kg are equal to Dita that makes the equation,
Equation 2 = > R + 2 = D or D – 2 = R
From the second equation, we can say that Rita weighs 2kg less than Dita.
Let’s solve both the equations to find Dita
Substitute the R in the 1st equation,
R + D = 8
(D-2) + D = 8
2D -2 = 8
2D = 8+2
2D = 10
D = 5
The answer is 5kg, hence D is the answer
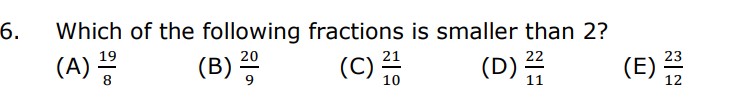
Let’s solve each options,
A) 19/8 = 2 3⁄8
Option A is greater than 2 so A is not the answer,
B) 20/9 = 2 2⁄9
Option B is greater than 2 so B is not the answer.
C) 21/10 = 2 1⁄10
Option C is greater than 2 so C is not the answer.
D) 22/11 = 2
Option D is equal to 2 so D is not the answer.
E) 23/12 = 1 11⁄12
Option E is less than 2 so E is the answer.

Given,
John’s garden has either a plant with 5 Leaves only or 2 Leaves and 1 Flower.
As the problem states, we need a total of 32 leaves and 6 flowers. We know that only one of the plants has a flower so there has to be 6 of that plant.
6 ( 2 leaves and 1 flower ) = 12 leaves and 6 flowers
Now we can subtract 12 leaves and 6 flowers from 32 Leaves and 6 flowers to find out how many more leaves we need.
32 Leaves and 6 flowers – 12 leaves and 6 flowers = 20 leaves
Therefore we need 20 more leaves
4(5 leaves) = 20 leaves
So that means, there should be 4 of the plants that have 5 leaves.
We need to find the total number of plants in John’s garden and we can find that by adding both equations.
6 ( 2 leaves and 1 flower ) + 4(5 leaves) = 32 Leaves and 6 flowers
6 + 4 = 10 plants
A is the answer.

Given,
Alva has 4 paper strips of the same length, when she glues 2 of them together with a 10cm overlap she gets a strip 50cm long.
We know that the strip is 50cm long, so let’s find out how long one strip is
50 – 10 = 40
40/2 = 20
20 + 10 = 30
So one strip must be 30 cm long
So both the strips must be equal to 60 and the 10cm overlap created a strip that is 50 cm long ( 60 – 10) given this we have to find out the overlap for a strip 56cm long
So we can subtract 60 – 56 making the overlap 4 cm long
Thus, A the answer

Given:
1)Adjacent flowers are spaced at the same distance apart.
2)The distance between the 1st Flower and the 3rd Flower is 60 cm.
So, let’s find the distance between the 1st and 2nd flowers. Since the distance between the 1st Flower and the 3rd Flower is 60 cm, and there are two gaps between them, we can divide 60 by 2 to determine the distance of one gap. Therefore, the distance between the 1st Flower and the 2nd flower is 30 cm.
Now, we can calculate the total distance between the 1st Flower and the 9th Flower and since there are 8 gaps, each 30 cm wide, we can multiply 30 by 8, giving us 240 cm.
So, we now know that the distance between the 1st Flower and the 9th Flower is 240 cm, which is equivalent to 2 meters and 40 cm.
Therefore, making the answer D) 2.4 meters
Let’s break down the information given in the problem:
– Lisa has 90 marbles.
– Anna has 10 more marbles than Lisa.
– Anna has 50 less marbles than Olle.
From these statements, we can find the number of marbles each person has:
Lisa has 90 marbles.
Anna has 90 + 10 = 100 marbles.
Olle has 100 + 50 = 150 marbles.
Now, we want to find out how many marbles they have together:
Total marbles = 90 + 100 + 150
Total marbles = 340
So, together, they have 340 marbles, making E the answer.

Given :
1)The rectangle ABCD is constructed of 4 identical rectangles
2)The length of BC is 1 cm.
To find the length of segment AB, we need to account for the two widths of the rectangles and one length of a rectangle.
But, before we do this we need to figure out the width of the rectangles. Looking at the image we see that two of the widths give us our length (1cm ) So that must mean a width is equal to (½) 0.5cm .
So, with this we can create the equation :
2 * 0.5 cm + 1 cm = 1 cm + 1 cm = 2 cm
hence, C is the answer

Given :
1)Lucy and her mother were both born in January.
2)Lucy adds the year of her birth, the year of her mother’s birth, her age, and her mother’s age on March 29 2015.
Let’s make the year Lucy was born as X
Now, to find the age of lucy we would subtract X from 2015, thus creating the equation 2015 – X
Accordingly, let’s make the year lucy’s mom was born as Y
And once again to find the age of lucy’s mom we would subtract Y from 2015, creating the equation 2015 – Y
We know that Lucy adds the year of her birth, the year of her mother’s birth, her age, and her mother’s age.
So that means lucy adds (2015- X) + (2015 – Y ) + X + Y
We can cancel out The X’s and The Y’s giving us 2015+2015 which is equal to 4030 making C the answer.

Given :
The area of the rectangle is 12 cm2.
The rectangles sides are integers.
To find the possible values for the perimeter of a rectangle with an area of 12 cm², we can start by listing the factor pairs of 12 (since area = length × width) and then see if these factors can be used as the lengths of the sides of the rectangle.
The factor pairs of 12 are:
1 × 12
2 × 6
3 × 4
4 x 3
6 x 2
12 x 1
Now, we’ll consider the perimeter for each of these factor pairs:
For the factor pair 1 × 12: Perimeter = 2 × (1 + 12) = 2 × 13 = 26 cm
For the factor pair 2 × 6: Perimeter = 2 × (2 + 6) = 2 × 8 = 16 cm
For the factor pair 3 × 4: Perimeter = 2 × (3 + 4) = 2 × 7 = 14 cm
For the factor pair 12 x 1: Perimeter = 2 × (12 + 1) = 2 × 13 = 26 cm
For the factor pair 6 x 2: Perimeter = 2 × (6+ 2) = 2 × 8 = 16 cm
For the factor pair 4 x 3: Perimeter = 2 × (4 + 3) = 2 × 7 = 14 cm
So, the possible values for the perimeter of the rectangle are 16 cm ,14 cm and 26cm.
We see 26 cm as one of answer choices making B the answer.

Given:
1) Each of the 9 line segments are either blue, green or red.
2) The 3 sides of each triangle are 3 different colors.
We see that in the given diagram there are 4 triangles which have connected to give us a parallelogram.
Lets label each of these triangles 1 – 4, where triangle 1 is the leftmost one and triangle 4 is the rightmost one.
We know that the 3 sides of each triangle are 3 different colors, so looking at triangle 1 and 3 we see that in both triangles the bottom edge is red, and so because of this in triangle 2 the 2 sides which are connecting triangles 1 and 3 should be green and blue because if 1 sides is red that means that in 1 triangle 2 sides would be red which would contradict the information given.
So, if the other 2 sides are blue and green that means X should be equal to red
Hence, C is the answer!

The equation X + X + YY = ZZZ is a mathematical equation where the variables X, Y, and Z represent digits, and you are trying to find values for these digits that satisfy the equation. This type of problem is often referred to as a “cryptarithmetic puzzle” or “alphametic puzzle.” The goal is to assign unique digits to each letter (X, Y, and Z) in a way that makes the equation true.
Given :-
X,Y and Z represent different digits
With this information we can say that :
X is any number between 0 and 9.
YY is any number between 10 and 99, we can even simplify this even more, since YY is a 2 digit number in which the number in both the tens and ones place are the same. So YY can be equal to the first 9 multiples of 11. So, YY can be any of { 11,22,33,44,55,66,77,88,99 }
Now, let’s see what the highest answer we can get. Now to do this we can add 9,9 and 99 ( X , X and YY. Once we add those numbers we get 117, now 117 cannot be equal to ZZZ because all the numbers aren’t equal. Now with this we can say that Z = 1, and ZZZ = 111, Because our answer is not going to be greater than 100.
With this we can also simplify what YY is equal to.
YY – 77,88,99
Now we can substitute with the following equation.
2X = 111 – YY
So, let’s start by substituting YY with 77 …
2X = 111 – 77
2X = 34
X= 17
X cannot be equal to 17 because 17 is greater than 9
Now lets substitute YY with 88
2X = 111 – 88
2X = 23
X= 11.5
X cannot be equal to 11.5 because 11.5 is greater than 9
Now lets substitute YY with 99
2X = 111 – 99
2X = 12
X = 6
So that means X = 6
Making E the answer!

To solve this problem, you need to determine which square to remove from the net so that the remaining squares can be folded into a cube. The net for a cube typically consists of 6 squares, with each square representing a face of the cube.
Given :
There are 7 squares in the paper net
A cube has 6 faces
To solve this puzzle, you can use graph theory and Euler’s characteristic formula, which is based on the number of vertices, edges, and faces in a 3D shape. For a cube, the formula is:
V – E + F = 2
Where:
V is the number of vertices,
E is the number of edges, and
F is the number of faces.
In a standard cube, you have:
V = 8 (8 vertices)
E = 12 (12 edges)
F = 6 (6 faces)
Now, in Carla’s situation, she drew 7 squares instead of 6. So, you have:
F = 7 (7 faces)
To make the figure connected and foldable into a cube, you need to determine which square to remove. Since you have an extra face, you should remove one of the squares to match the standard cube’s 6 faces. Removing one square means:
F = 6
Now, you can use Euler’s formula to find the number of vertices (V) and edges (E) required to maintain a connected shape:
V – E + F = 2
Solving for V – E:
V – E = 2 – F
V – E = 2 – 6 V – E = -4
So, you need to have 4 fewer edges than vertices. Now, to maintain connectivity, you can determine which square to remove in such a way that it removes 4 edges. You need to select a square where removing it will eliminate 4 edges from the network. This square should be one that’s connected to the other squares through these 4 edges.
Given our paper net we can remove the squares with numbers 4,7,1 and 3
We can not remove 1 because 1 is an corner piece and connects 6 and 2
We can not remove 4 because if we remove 4 we won’t have the top face of our cube
We can remove 7 or 3 because if we remove 7 or 3 the remaining paper net will fold to make a cube

To solve this problem we can use a tree diagram.
A tree diagram is simply a way of representing a sequence of events. Tree diagrams are particularly useful in probability since they record all possible outcomes in a clear and uncomplicated manner.
Let’s break down the given operations:
Start with the number 100.
Multiply by 2 or 3:
You can choose to multiply 100 by 2 or by 3.
Possibilities:
100×2=200
or
100×3=300
Increase the result by 1 or 2:
You can choose to add 1 or 2 to the result obtained from the previous step.
For 200 We have 2 possibilities,
200+1=201
or
200+2=202
For 300 We also have 2 possibilities,
300+1=301
or
300+2=302
Divide the new result by 3 or 4:
You can choose to divide the result obtained from the previous step by 3 or by 4.
For 201, we have 2 possibilities:
201÷3=67
201÷4=50.25 (not a natural number).
For 202,, we have 2 possibilities:
202÷3=67.33 (not a natural number)
202÷4=50.5 (not a natural number).
For 301, we have 2 possibilities:
301÷3=100.33 (not a natural number) or
301÷4=75.25 (not a natural number).
For 302, we have 2 possibilities:
302÷3=100.67 (not a natural number) or
302÷4=75.5 (not a natural number).
So the only number that is a natural number is 67 hence C the answer.

Given –
ABCD are in increasing order from left to right.
Now logically thinking B has to be the largest number because it’s the first number in the equation. Now B can not be 9 because then C will be 10 which is a 2 digit number. Similarly B cannot be 8 because then D will be 10 which is once again a 2 digit number. So that means B is equal to 1.
Now just like B being the largest number A has to be the smallest number because then only we will get the largest number possible in our tens place. So A has to be 1.
Now C and D have to be 8 and 9 because B is equal to 7 and according to the rule “ABCD are in increasing order from left to right. And after 7 comes 8 and 9!
Now, substituting these values into the expression : T
BD – AC we would get :
79 – 18 which is equal to 61 making B.

This Problem falls under the category of geometry, specifically perimeter calculations. Perimeter is the total length of the boundary of a shape, so in this case, you would need to determine how the squares are arranged and then calculate the sum of the lengths of the sides of the outer boundary of the composite shape.
Given :
1) Tom used 6 cubes of sides length 1
Now in the given shape, we see 10 full sides, and we know that these sides are of length 1. Additionally, we can observe 4 sides, which do not take up the whole length of 1.
Looking at the bottom layer we see that the length is 3, now looking at the second layer we see that the length is 2 so the gap must be 1.
Once again we see that in the second layer the length is 2cm and in the first layer the length is 1 so once again the gap must be 1.
10(1) + 1 + 1 =
12
Making B the answer!

This problem involves algebra and the manipulation of algebraic expressions. The approach used here is based on setting up equations to represent the relationships between the perimeters of the smaller and larger sheets, and then solving for the variables involved (length and width of the sheets).
Given :
1) Square paper sheets of 2 sizes are needed.
2) The larger sheet is 8 times greater than the smaller sheet.
Let’s denote the side length of the smaller square sheet as s and the side length of the larger square sheet as S.
The perimeter of a square is given by the formula:
Perimeter= 4 × Side Length
So, for the smaller sheet, the perimeter is 4s, and for the larger sheet, the perimeter is 4S.
The problem states that the perimeter of the larger sheet is eight times as great as the perimeter of the smaller sheet:
4S=8×(4s)
Now, let’s solve for S in terms of s:
4S=32s
S=8s
Now, if there are 8 smaller squares along each side of the larger square, the number of smaller squares in the larger square can be found by multiplying the number of smaller squares along one side (8) by the number of smaller squares along the other side (also 8). This corresponds to using the area formula for a square:
Number of smaller squares = Number of squares along one side × Number of squares along the other side
Number of smaller squares=8×8=64.
So, using this method, we also find that 64 of the smaller square sheets are needed to cover one of the larger square sheets.
Making A the answer!

So, this problem relies more on logical deduction and strategic arrangement rather than a specific mathematical formula or method. It involves reasoning and understanding the constraints to find the best arrangement that maximizes the number of inhabitants.
Given –
– Any two neighboring houses together are inhabited by at most six people
– At least one person lives in each house.
– On Jump Street, there are 9 houses in a row
To maximize the number of people on Jump Street under the given conditions, we need to distribute the people across the houses in a way that adheres to the constraint that any two neighboring houses together can have at most six people.
To reach a sum of 6, there are five possible sets: 5 + 1, 2 + 4, 3 + 3, 4 + 2, and 1 + 5. S
Since there are 9 houses and 9 is an odd number so the 1st number will also be the last number.
Considering that all the sets equal 6, with four sets of “6’s” in 9, the last number becomes the tiebreaker, and it must be the largest. Considering that there are four sets of “6’s” in the 9 houses, the final number becomes the determining factor, favoring the set with the highest last number.
So, selecting the set 5 + 1, where 5 is the larger number, we get the following arrangement:
5+1+5+1+5+1+5+1+5= 29.
In conclusion, by strategically arranging the sets that sum to 6 and considering the odd number of houses, the logical deduction leads us to the understanding that the largest number of people that could be living on Jump Street, while adhering to the given constraints, is 29.
Hence D is the answer!

The method used to solve this problem is a system of linear equations. You set up equations based on the given information and relationships between the variables and then solve the system to find the values of the variables.
Given :
– Tom and Bob caught 42 mice in three days.
– Tom caught twice as many mice as the previous day.
– Bob caught two more mice than in the previous day.
– Both cats caught the same number of mice for the three days.
First, it says that Tom and Bob caught 42 mice in three days, this can be expressed as :
T + B = 42
Then we have how many mice caught Tom each day, which can be expressed as:
T = T1 + T2 + T3
With T1 being the number of mice Tom caught on the first day, T2 the number of mice Tom caught on the second day and T3 the number of mice Tom caught on the third day.
The problem states that Tom caught twice as many mice as the previous day, So, T2 is 2 times T1 and T3 is 2 times T2 or 4 times T1 :
T3 = 2T2
T2 = 2TI
Replacing this into equation 1 :
T = T1 + 2TI +2T2 = T1 +2T1 + 4T1
Thus, T = 7T1
Then we have how many mice caught Bob:
B = B1 + B2 +B3
With B1 being the number of mice Bob caught on the first day, B2 the number of mice Bob caught on the second day and B3 the number of mice Bob caught on the third day.
The problem says that Bob caught two more mice than the previous day, so B2 is B1 + 2 , and B3 is B2 + 2 or B1 + 4 :
B2 = B1 + 2
B3 = B2 + 2
Replacing into our previous equation :
B = B1 + B1 + 2 + B2 + 2
Which is equal to :
B = B1 + B1 + 2 + B1 + 2 + 2
And we can simplify it into :
B = 3B1 + 6
Finally, we know that they both caught the same amount of mice during the three days:
T + B = 42
Given The information that Tom and Bob caught the same number of mice T and B are equal to 42/2. Thus Tom and Bob caught 21 mice each.
So, If T = 7T1, and 7T1 = 21. Then T1 = 3. Thus, Tom Caught 3 mice on day 1.
Similarly,
B = 3B1 + 6 and 3B1 + 6 = 21
So, If 3B1 + 6 = 21. Then B1 = 5. Thus, Bob caught 5 mice on day 1
So the amount of mice caught on the first day is:
T1 + B1 = 3 + 5 = 8
Hence, C is the answer.

This problem involves using algebraic methods, specifically solving a system of linear equations, to determine the number of balloons each child is holding. Let’s assign variables to represent the number of balloons each child has:
– A for Andrew
– B for Bob
– C for Clara
-D for Danny
– E for the fifth child
The given information is as follows:
1. (A + B + C + D + E = 37)
2. (B + C + D + E = 14) (to the right of Andrew)
3. (C + D + E = 32) (to the right of Bob)
4. (D + E = 20) (to the right of Clara)
5. (E = 8) (to the right of Danny)
By substituting (E = 8) into equation 5, we find (D + 8 = 20), leading to (D = 12). Next, substituting (D = 12) into equation 4 : (C + 12 = 20), we find (C = 8).
Therefore, Clara indeed holds 8 balloons, making (C) the answer.

This problem requires using algebraic equations to represent relationships between numbers on a cube’s faces and spatial visualization to understand the geometric arrangement of vertices and faces in solving the puzzle.
Let’s reconsider the information given:
vertex C, is equal to 14.
Vertex D is equal to 16.
Vertex E is equal to 24.
To start this problem let us make an net of this cube :
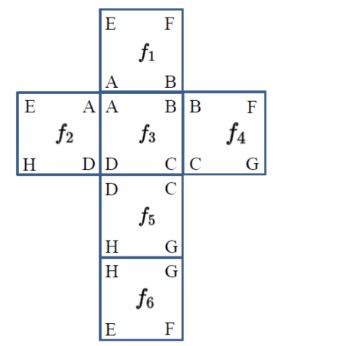
For Vertex D : 16 = F2 + F3 + F5
For Vertex C : 14 = F3 + F4 + F5
SO D – C = F2 + F3 + F5 – (F3 + F4 + F5 )
2 = F2 – F4
Corner F : F = F1 + F4 + F6
Corner E : 24 = F1 + F2 + F6
So F – E is F1 + F4 + F6 – ( F1 + F2 + F6 )
F – 24 = F4 – F2
F = 24 + F4 – F2
We know that F2 – F4 equals 2, so since the numbers are flipped we would get F4 – F2 equal to – 2 .
F = 24 + (-2)
F = 22
Thus making C our answer!

This problem is solved using algebraic reasoning. By defining variables to represent the coach and compartment numbers for both Mike and Jane, we create equations based on the given information.
Let’s analyze the information given:
1. Mike is in the third coach and the 18th compartment from the engine.
2. Jane is in the seventh coach and the 50th compartment from the engine.
Since there are 12 coaches, we can represent Mike’s position as (Coach 3, Compartment 18) and Jane’s position as (Coach 7, Compartment 50).
Now, let’s find the number of compartments in each coach:
The difference in the coach numbers between Mike and Jane is 7 – 3 = 4 coaches.
The difference in the compartment numbers between Jane and Mike is 50 – 18 = 32 compartments.
Since each coach has the same number of compartments, we can find the number of compartments in each coach by dividing the total difference in compartments by the total difference in coach numbers:
Number of compartments in each coach = Total difference in compartments / Total difference in coach numbers
Number of compartments in each coach = 32 / 4
Number of compartments in each coach = 8
Therefore, there are 8 compartments in each coach making B the answer!

The problem involves combinatorics, specifically permutations with restrictions. We need to find the number of ways to arrange three kangaroos (K) and four empty spaces (E) in a line of seven cells such that no two kangaroos are neighbors.
To solve this problem, let’s consider the possible arrangements for placing the three kangaroos in three different cells such that no two kangaroos are neighbors.
Let’s represent the kangaroos as K and the empty cells as _ , we want to arrange KKK into _ _ _ _ _ _ _ in such a way that no two K’s are adjacent.
Here are the possible arrangements:
1. K _ K _ K _ _ (1)
2. K _ K _ _ _ K (2)
3. K _ _ _ K _ K (3)
4. _ _ K _ K _ K (4)
5. K _ _ _ K _ K (5)
6. K _ K _ K _ E (6)
7. _ _ K _ K _ K (7)
8. K _ K _ _ _ K (8)
9. K _ _ _ K _ K (9)
10. K _ K _ K _ _ (10)
So, there are 10 ways to place the three kangaroos in three different cells such that no two kangaroos are neighbors.
Therefore, the correct answer is (D) 10.

Given :
1) The distances between them are, in increasing order.
2) Four points lie on a line.
Now, to solve this problem we need to use our knowledge about inequalities. Inequalities in mathematics are expressions that compare the relative sizes of two values, using symbols such as < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to). Solving inequalities involves determining the possible range of values for a variable that satisfies the given conditions expressed in the inequality.
These represent the distances between consecutive points on a line. The differences between consecutive distances are: 1, k−3,11−k, 1, 2.
To maintain the order, k−3 must be less than or equal to 1, and 11−k must be less than or equal to 2.
So now we have two inequalities :
k − 3 ≤ 1 (the difference between the second and third distances should be smaller than or equal to the difference between the first and second distances).
11 − k ≤ 2 (the difference between the fourth and fifth distances should be smaller than or equal to the difference between the third and fourth distances).
Now, solving these inequalities:
K −3 ≤ 1 implies
K ≤ 4.
11− K ≤ 2 implies
K ≥ 9.
Combine the results:
4 ≤ k ≤ 9 .
The only option within this range is k = 9.
So, the correct answer is (E) 9.

The problem applies spatial geometry principles to construct a cube measuring 4 by 4 by 4, using unit cubes with a side length of 1.
Given :
1) He, painted 3 faces of the big cube red and the other 3 faces blue.
2) After he finished,there was no small cube with 3 red faces.
We know that Basil used small cubes with side 1 to create a larger cube with side 4. This means that the larger cube is formed by arranging (4 * 4 * 4) small cubes, resulting in a total of (64) small cubes.
Basil painted 3 faces of the big cube red and the other 3 faces blue. Each face of the big cube consists of (4 * 4 = 16) small cubes, so painting 3 faces means (3 * 16 = 48) small cubes are painted either red or blue.
The problem states that there is no small cube with 3 red faces. This implies that each small cube can have at most 2 faces painted.
Since each small cube can have at most 2 faces painted, and there are a total of (48) small cubes painted either red or blue, the number of small cubes with both red and blue faces is (48 \ 2 = 24).
In summary, the correct answer is (D) 24 small cubes have both red and blue faces. This is because each of the (48) painted small cubes can contribute 2 faces to the count of small cubes with paint, and thus (48 \ 2 = 24) small cubes have both red and blue faces.

Recent Comments