
Finding the candle that blew out first is the challenge at hand. After reading the question, we can tell that Akira was lighting her candles. A taller bar indicates that the candle blew out first, since the provided photo illustrates how tall the candle was when it did so.
We must concentrate on the tallest bar in order to get the solution. The candle blew out faster on taller bars. This is because a shorter bar indicates that more time was spent, indicating that the candle was lit for a longer amount of time.
Candle D is the largest of the five, as can be seen by closely examining the graph. In comparison to the other candle, this indicates that candle D blew out first.
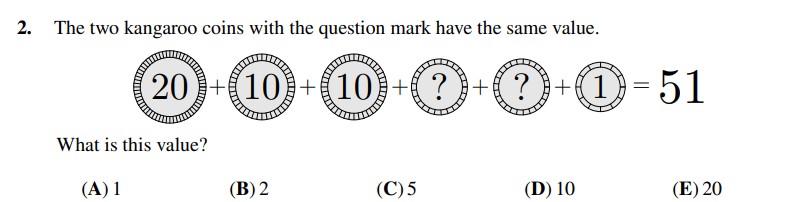
We can represent two question marks as 2x if they have the same value, where “x” is the value of each question mark. After that, the equation is:
51 is 20 + 10 + 2x + 1.
Simplify the known numbers first:
20 + 10 + 1 = 31.
The total of the two question marks may now be found by subtracting 31 from 51:
51 minus 31 equals 20.
We have 2x = 20 since the values of the two question marks are equal. Divide both sides of the equation by two to determine the value of x:
20 ÷ 2 x = 10 = 2x = 20 x = 20.
Therefore, each question mark has a value of 10. The formula turns into:
51 is equal to 20 + 10 + 10 + 10 + 1.
This is effective because we use 2x to describe the same value that both question marks signify.
Thus, the answer to this problem is D)10.
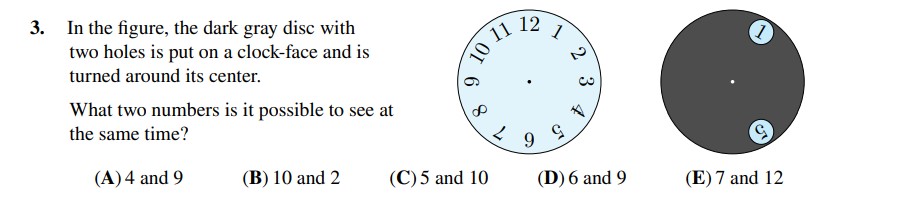
In this problem, we are shown a clock face with a black disk covering two numbers, and we need to identify which numbers are hidden.
We know that the numbers in between the hidden numbers are 2, 3, and 4. This means the gap between the two hidden numbers includes these three numbers.
Now, let’s examine the answer choices:
4 and 9: The numbers between 4 and 9 are 5, 6, 7, and 8, which is a gap of 4 numbers. So this can’t be the answer.
10 and 2: The numbers between 10 and 2 are 11, 12, and 1, which are only 3 numbers. This matches the condition, so this could be the correct answer.
5 and 10: The numbers between 5 and 10 are 6, 7, 8, and 9, which is a gap of 4 numbers. So this can’t be the answer.
6 and 9: The numbers between 6 and 9 are 7 and 8, which is only 2 numbers. So this can’t be the answer.
7 and 12: The numbers between 7 and 12 are 8, 9, 10, and 11, which is a gap of 4 numbers. So this can’t be the answer.
The correct answer is 10 and 2, as there are exactly 3 numbers between them (11, 12, and 1), matching the condition given in the problem.

Understanding the Pieces
Each piece is an “L” shape but with different arm lengths and orientations:
Piece 1: A larger “L” shape with arms extending to the left and upward.
Piece 2: Another large “L” shape, but with arms extending to the right and upward.
Piece 3: A large “L” shape with arms extending to the right and downward.
Piece 4: A smaller “L” shape with arms extending to the right and downward.
To form a square, the two chosen pieces must fit perfectly together without leaving gaps or overlapping. Additionally, the combined pieces’ outer edges must form a clean square boundary.
Testing Each Combination
Option A: Pieces 1 and 2
At first, it seems like these pieces might work since they are oriented in opposite directions. However, when you try to fit them together, their arms don’t align properly. Even if rotated, these two pieces leave gaps in the square boundary because one piece’s arm is always too long or too short compared to the other.
❌ This pair does not form a square.
Option B: Pieces 1 and 3
Both pieces are large “L” shapes but face in different directions. When you try to combine them, the issue becomes clear: their arms either overlap or leave gaps, depending on how they are rotated. The two shapes don’t complement each other in a way that forms a square.
❌ This pair does not form a square.
Option C: Pieces 1 and 4
Now, let’s consider this pair. Piece 1 is a large “L” shape, while Piece 4 is a smaller “L.” When Piece 4 is rotated, its arms align perfectly with the edges of Piece 1. The longer arm of Piece 1 fills in the gap left by the shorter arm of Piece 4, and vice versa. Together, these two pieces create a seamless square with no gaps or overlaps. This is the only pair that works.
✅ This pair fits perfectly to form a square.
Option D: Pieces 2 and 3
At first glance, it might seem like these pieces could fit together, but upon testing, it becomes evident that they do not. Their arms fail to align properly, leaving gaps no matter how they are rotated. These two pieces cannot form a clean square boundary.
❌ This pair does not form a square.
Option E: Pieces 2 and 4
Finally, we test this pair. Piece 2 is a large “L,” while Piece 4 is a smaller “L.” While their shapes are somewhat complementary, their arms do not align properly to create a seamless square. Even with rotation, gaps remain between the pieces, preventing them from forming a perfect square.
❌ This pair does not form a square.
Conclusion
After carefully testing each pair of pieces, the only combination that works is Pieces 1 and 4. When Piece 4 is rotated, it aligns perfectly with Piece 1 to form a square with no gaps or overlaps. This solution requires observing how the pieces complement each other and experimenting with rotations to find the perfect fit. Therefore, the correct answer is C: Pieces 1 and 4.

Holger is filling the table with numbers, starting from 1, row by row. Our task is to figure out which shape (A, B, C, D, or E) matches the table after it’s completely filled. Let’s find the solution by spotting simple number patterns in the table.
The table follows a pattern. Each row has 10 numbers. For example, the first row goes from 1 to 10, the second row from 11 to 20, and the third row from 21 to 30. To move down within the same column, you add 10 to the number (e.g., 22 → 32 → 42). To move right in the same row, you add 1 (e.g., 22 → 23 → 24). Using these patterns, we can check whether each shape fits.
Let’s start with Shape A. This shape begins with 22, moves down to 32 (add 10), then moves right to 33 (add 1), and finally down to 44. However, moving from 33 to 44 doesn’t follow the expected pattern because moving down should add 10, not 11. Therefore, Shape A does not fit the table.
Next is Shape B. It starts at 22 and moves diagonally down to 33 (add 11). However, this move doesn’t match the pattern of adding 10 to move down. Therefore, Shape B also doesn’t fit.
Shape C is different. Starting at 22, it moves down to 32 (add 10), then right to 33 (add 1), and finally down to 43 (add 10). Every move in this shape matches the table’s pattern perfectly. This means Shape C works!
For Shape D, the numbers start at 22 and move diagonally to 33 (add 11), but this step breaks the rule of moving down by adding 10. This makes Shape D incorrect. Lastly, Shape E starts at 22, moves down to 32 (add 10), then right to 33 (add 1), and finally down to 42. While most of the moves fit, moving from 33 to 42 doesn’t follow the correct pattern. So, Shape E is also incorrect.
In conclusion, the only shape that matches the table is Shape C! By noticing simple patterns like adding 1 to move right and adding 10 to move down, we can solve puzzles like this easily.

Recent Comments